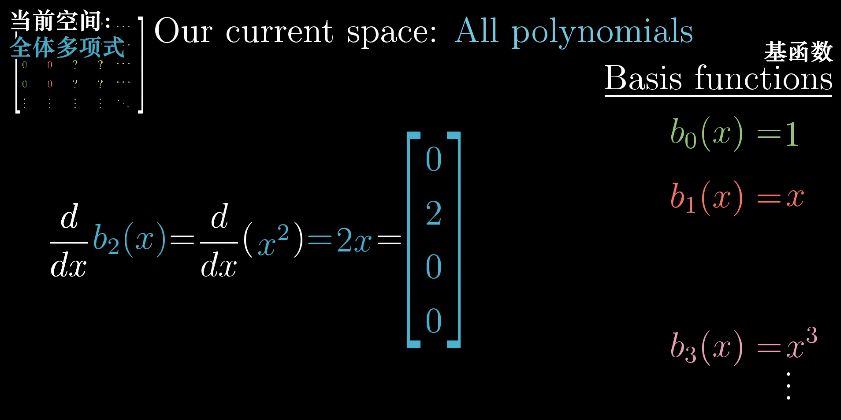Essence of linear algebra

07 Apr 2018

前言

以下内容启发自著名youtuber-3b1b的线代教程。不涉及到具体计算方法，只对线代的基本几何意义进行总结。

1 线性

• 线性相关：a可用b（可能由多个线性无关的向量组成）表示出来
• 线性变换：向量空间的线性函数变换，其中的空间变换关系就是矩阵，矩阵中的具体数值可看作原基向量通过这种变换后的坐标位置
• 矩阵的行列式的绝对值含义为线性变换使空间压缩或放大的比例，如果行列式为负，则表示将空间翻转了，空间定向（orientation）改变了。特征就是本来在单位向量i左边的j，转到了i右边。
• 转置不改变行列式的值。
• 行列式为0，代表着原空间维度的损失。

2 秩与线性方程组

• 一个矩阵将原空间的线性变化后，该矩阵的秩就是变换后空间的维度。
• 求解线性方程组$Ax=v$的答案 $x$（$x=A^{-1}v$）,x和v是被矩阵A线性变换前后的向量，所以求解x就是将v反向变换回来的操作，所以$A^{-1}A=I$。
  • 如果线性方程组中的$A$不存在逆矩阵（即其不满秩），那只有$v$在$A$将原空间线性变换后的空间上时，$x$才能有解。
  • 满秩矩阵才存在逆矩阵，逆矩阵就是原矩阵进行的空间线性变换的反向操作；也就是说，如果矩阵将空间变换后的维度降低了，那就不存在某种逆变换能够将空间还原。
  • 满秩意味着秩与列数相等；若方阵$A$的$R(A)=n$，称$A$为满秩矩阵（可逆矩阵，非奇异矩阵）。
• 求解线性方程组$Ax=0$的答案，从几何的角度来考虑，$A$将原空间维度降低了，找到原空间中的某个向量$x$，$x$必须和变换后的新空间垂直。
• 矩阵的列是原空间基向量变换后的位置；矩阵的 列空间 是矩阵在将空间线性变换后，所有通过原点的向量的集合共同张成的空间，也就是矩阵的列所张成的空间。
• 对于方阵有：非奇异矩阵 = 满秩矩阵 =可逆矩阵，奇异矩阵 = 降秩矩阵。

3 核Kernel

• 通过矩阵的变换后落在原点的向量的集合(该过程伴随着维度降低，即矩阵不满秩)，被称作矩阵的“零空间”(Null space)或“核”（Kernel）；
• 向量集合张成的空间就是“零空间”，“零空间”和矩阵变换后的空间相互垂直。
• 线性方程组$Ax=0$(0向量)的解$x$，就是零空间。

4 非方阵

• 行m > 列n 的非方阵，表达的变换，是将输入空间的n个基向量变换到高维(m)空间中的一部分(一个n维空间)表示出来。
  • 例子1. m=3,n=2 是将原2维平面空间变换到3维空间中的某个平面上。
    • 该矩阵依然满秩，因为列空间的维度和输入空间的维度相等，原输入空间二维，经过矩阵变换输出后，空间依然二维！
  • 例子1. m=2,n=3 是将原3维空间压缩到2维空间（试想象在该矩阵右边乘上一个3x1的向量）。
    • 该矩阵不满秩（可能行满秩），因为列空间的维度 2 小于输入空间的维度 3。

Q:$R(A)\leq min(m,n)$? 2x3的矩阵就是不(列)满秩的？意味着空间变换的时候有维度的损失？自问自答：yes,yes,yes.

5 点积（内积）与对偶

对偶性:两种数学事物之间自然而又出乎意料的对应关系。

你可以说一个向量的对偶是其定义的线性变换；一个多维空间到1维空间的线性变换的对偶是多维空间的某个特定向量。

• 下列两个矩阵的空间变换效果相同，都是垂直拍平2维空间，去掉一个维度:

$$\begin{bmatrix} 1&0 \end{bmatrix}\& \begin{bmatrix} 1&0 \\ 0&0 \end{bmatrix}$$

• 将向量看作一种线性变换（矩阵）。1x2矩阵就是一种将二维空间变换为一维数轴的过程，该过程可以看做将2维空间的向量线性变换为一维空间的数值：

$$\begin{bmatrix} a&b \end{bmatrix} \begin{bmatrix} x\\ y\end{bmatrix} =ax+by$$

• 两个向量的点积是其中一个向量（任意）在另一向量上的投影的长度与被投影向量的长度乘积:

$$\begin{bmatrix} a\\ b \end{bmatrix} . \begin{bmatrix} x\\ y \end{bmatrix} =ax+by$$

1x2矩阵和二维向量相乘的计算过程 和 其相应的转置矩阵求点积的计算过程相同，这个点积的投影过程就是矩阵的线性变换映射的过程

6 叉积（外积）

• 两个向量的叉积只能定义在3维空间内。
• 叉积：两个向量 $\vec v,\vec w​$ 的叉积是一个向量，该向量垂直于a和b所在的平面，方向由右手法则确定。向量的长度为a和b围成的平行四边形的面积。

引入一不确定的向量$\vec a=\begin{bmatrix}x&y&z\end{bmatrix}^T$和 $\vec v,\vec w$ 一起组成矩阵$\begin{bmatrix}\vec a&\vec v&\vec w\end{bmatrix}^T$并计算其行列式。行列式的值就是三个向量围成的平行六面体的体积。此时寻找一个$\vec p$使得：

$$\begin{bmatrix} p_1\\ p_2\\ p_3 \end{bmatrix}\cdot \begin{bmatrix} x\\ y\\ z \end{bmatrix}=det \left( \begin{bmatrix} x&v_1&w_1\\ y&v_2&w_2\\ z&v_3&w_3 \end{bmatrix} \right)$$

上式左侧是3维空间里两个向量的点积，可看做$\vec a$投影在$\vec p$上的长度乘以$\vec p$的长度。式子等号若要成立，可看作以$\vec v,\vec w$围成的平行四边形为底，为其寻找一个垂直于该四边形平面的向量$\vec p$，该向量的长度等于平行四边形的面积：

7 基变换

• 基向量是空间内一组用来描述向量的作为单位的向量。在我们当前的视角下基向量一般都是选用相互垂直的单位向量$I$。
• 若在某基向量$X$(也是基于我们当前视角下的基向量$I$描述出来的$X$)下描述的一向量${\vec a}^x$想转化为我们的视角下的向量${\vec a}^{I}$，可以利用下述公式进行转换：

$${\vec a}^{I}=X{\vec a}^{X}$$

​ 注意：${\vec a}$是客观存在的一不需要用基来描述的向量；在基向量$X$下描述出的向量 ${\vec a}$ 是 ${\vec a}^{X}$，其本质是在$X$视角下的对基向量的选用方式，并且$X$矩阵中的具体数值是用我们当前的视角（$I$）描述出的。所以上式左边的向量就是我们当前视角下的向量${\vec a}^I$

• 如果我们想把当前视角下的${\vec a}^I$转化为基向量$X$视角下的向量（${\vec a}^X$）来表示出来，可以用如下方法：
  ${\vec a}^{X}=X^{-1}{\vec a}^{I}$

• 将我们当前基向量$I$视角下的某种变换$A^I$用另一种基向量视角$X$来表述出来: $A^X=X^{-1}A^IX$。如果当前基向量视角下有某个向量${\vec a}^I$进行矩阵$A^I$的变换，然后用基向量$X$描述出来：
  ${\vec a}^{X}=X^{-1}A^IX{\vec a}^{I}$ 所以，通常表达式$X^{-1}A^IX$暗示着一种数学上的转移作用，即视角上的转化

8 特征向量和特征值

• 特征向量：在经过矩阵的变换后，仍处于自己张成的空间内的向量。也就是矩阵的变换沿着特征向量的方向进行。

• 特征值：矩阵变换将特征向量放缩的倍数。 $A\vec v=\lambda\vec v$

  • $\lambda$和$\vec v$分别为矩阵$A$的特征值和特征向量，矩阵对空间内某个向量的变换，等价于该向量方向不变的放缩。
  • 求解方式是$det(A-\lambda I)\vec v=\vec 0$，即求$det(A-\lambda I)=0$。因为当且仅当矩阵代表的变换将空间压缩到更低的维度时（行列式为0），才会存在一个非零向量，使得矩阵和它的乘积为零向量。

• 有些矩阵没有特征向量，比如旋转矩阵$\begin{bmatrix}1&-1\1&1\end{bmatrix}$，所有原空间内的向量都离开了自己张成的空间(计算得出的特征值有复数，一般特征值为复数对应于变换中的某种旋转)；有些矩阵有无数个特征向量，比如放大矩阵\(\begin{bmatrix}2&0\0&2\end{bmatrix}\)，其只有一个特征值2。

• 对角矩阵：除了对角线上有非0值，其余位置数值全部为0。解读这种矩阵的方法是，所有基向量都是特征向量，对角线上的数值是对应特征向量的特征值（即可以理解为对角阵的特征值为对角元，特征向量组成的基为$I$）；所以对角矩阵与自身相乘$n$次的效果，就是将每个特征向量放大${\lambda}^n$倍，${\lambda}$为其对应的特征向量。

• 用特征向量来作为基向量，转化原空间内的一种矩阵变换为新的基向量视角下的矩阵变换：

  $$\begin{bmatrix} 1&-1\\ 0&1 \end{bmatrix}^{-1} \begin{bmatrix} 3&1\\ 0&2 \end{bmatrix} \begin{bmatrix} 1&-1\\ 0&1 \end{bmatrix}= \begin{bmatrix} 3&0\\ 0&2 \end{bmatrix}$$

  上式（$A^{-1}XA=D$）右边得出的矩阵变换，每列为特征向量，对角线数值为每个特征向量对应的特征值，可称这种特征向量构成的基向量组成的集合为“特征基”（eigenbasis）。

• 上诉变换过程为“对角化”，并非所有矩阵都能对角化，只有特征基能够张成整个空间才行，即特征向量个数达到整个空间的维度。

• 如果想求原始矩阵变换的100次幂，可现将其转变为用特征基来表示，然后在特征基的坐标系中计算其100次幂，然后再转换回原基表示。即$AD^{100}A^{-1}=X^{100}$。

9 抽象向量空间

普适的代价是抽象。

• 行列式和特征向量与所选坐标系无关，行列式表示的是变换对面积的缩放比例，特征向量是在变换中留在它所张成的空间中的向量。

• 微分算子$\frac{d}{dx}$是线性的，求导是线性运算。

  $$\begin{cases} L(\vec v+\vec w)=L(\vec v)+L(\vec w)\\ L(c\vec v)=cL(\vec v) \\ \\ \frac{d}{dx}(x^3+x^2)=\frac{d}{dx}(x^3)+\frac{d}{dx}(x^2)\\ \frac{d}{dx}(4x^3)=4\frac{d}{dx}(x^3) \end{cases}$$

• 关于向量的概念在函数的世界都有直接的类比：

  

• 只要处理的对象集具有合理的数乘和相加的概念，线性代数中所有关于向量、线性变换和其他的概念（线性变换、零空间、特征向量、点积等）都适用于它；这些类似向量的事物，如箭头、一组数、函数等，构成的集合被称作“向量空间”：

  

• 对于向量空间内的函数来说，微分算子$\frac{d}{dx}$就是一种线性变换。更具体地，对于函数中的全体多项式空间来说，基向量此时就是基函数：

  

  此时求导这种线性变换（微分算子$\frac{d}{dx}$满足线性性质）就可以用一个无限阶矩阵描述：

  

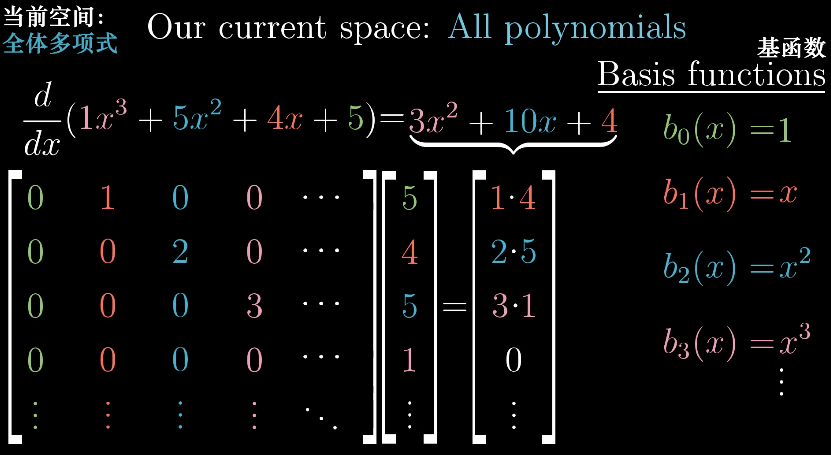
  其中微分矩阵的计算方法是，对每个基函数进行微分变换得出微分后的基函数，将所有基函数组合在一起就是相应的整体微分变换矩阵：