Basic data structure - binary tree & ADT
05 Oct 20161 简介
在计算机科学中,二叉树(英语:Binary tree)是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二元堆积。
二叉树的每个节点至多只有二棵子树(不存在度大于
2的节点),二叉树的子树有左右之分,次序不能颠倒。二叉树的第i层至多有2^(i−1)个节点;深度为k的二叉树至多共有2^(k+1)−1个节点;对任何一棵二叉树T,如果其终端节点数为n0,度为2的节点数为n2,则n0=n2+1。一棵深度为
k,且有2^(k+1)−1个节点称之为满二叉树;深度为k,有n个节点的二叉树,当且仅当其每一个节点都与深度为k的满二叉树中,序号为1至n的节点对应时,称之为完全二叉树。与树不同,树的节点个数至少为
1,而二叉树的节点个数可以为0;树中节点的最大度数没有限制,而二叉树节点的最大度数为2;树的节点无左、右之分,而二叉树的节点有左、右之分。
以上来自wiki百科
2 树的实现
用以下的函数创建并操作二叉树:
- BinaryTree() 创建一个二叉树实例
- getLeftChild() 返回节点的左孩子
- getRightChild() 返回节点的右孩子
- setRootVal(val) 把val变量值赋给当前节点
- getRootVal() 返回当前节点对象。
- insertLeft(val) 创建一个新二叉树作为当前节点的左孩子
- insertRight(val) 创建一个新二叉树作为当前节点的右孩子。
2.1 节点与引用方法
我们定义一个类,它的属性值包括根,和左右子树。因为这种方法更加面向对象。使用节点和引用,我们认为树形结构大致如下:
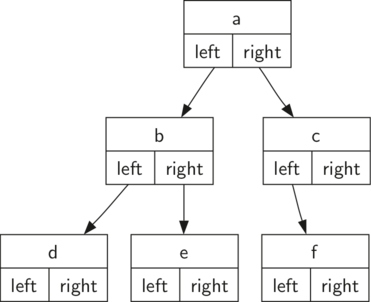
上图只是一个节点的定义和两个子树的引用。重要的是,左右子树的引用的,也是这个类的实例。例如,如果要插入一个新的左子树,那么创建一个新的树对象并且修改根节点的self.leftChild指向新树。
2.2 二叉树类的定义
__init__构造函数需要一个对象来保存在根节点。既然列表可以保存任意对象,那么树的根可以是任意对象。
插入左右子树要考虑两种情形:第一种是没有左孩子,只需把节点加到树上。第二种是此节点已经有左孩子,这时要把现存的左孩子下移一级作为插入节点的左孩子。
class BinaryTree(object):
def __init__(self, rootObj):
self.key = rootObj
self.leftChild = None
self.rightChild = None
def insertLeft(self, newNode):
if self.leftChild == None: # 新建
self.leftChild = BinaryTree(newNode)
else: # 插入更新
t = BinaryTree(newNode)
t.leftChild = self.leftChild
self.leftChild = t
def insertRight(self, newNode):
if self.rightChild == None: # 新建
self.rightChild = BinaryTree(newNode)
else: # 插入更新
t = BinaryTree(newNode)
t.rightChild = self.rightChild
self.rightChild = t
def getRightChild(self):
return self.rightChild
def getLeftChild(self):
return self.leftChild
def setRootVal(self, obj):
self.key = obj
def getRootVal(self):
return self.key
def preorder(self):
print(self.key)
if self.leftChild:
self.leftChild.preorder()
if self.rightChild:
self.rightChild.preorder()
2.3 代码测试
r = BinaryTree('root!')
print(r.getRootVal())#root!
print(r.getLeftChild())#None
r.insertLeft('leftTree!')
print(r.getLeftChild())#<__main__.BinaryTree object at 0x100c5a2b0>
print(r.getLeftChild().getRootVal())#leftTree!
r.insertRight('rightTree!')
print(r.getRightChild())#<__main__.BinaryTree object at 0x100c5a2e8>
print(r.getRightChild().getRootVal())#rightTree!
r.getRightChild().setRootVal('new_rightTree!')
print(r.getRightChild().getRootVal())#new_rightTree!
3 树的遍历
访问树的全部节点,一般有三种模式,这些模式的不同之处,仅在于访问节点的顺序不同。我们把这种对节点的访问称为“遍历”,这三种遍历模式叫做前序、中序和后序。
3.1 前序遍历
在前序遍历中,先访问根节点,然后用递归方式前序遍历它的左子树,最后递归方式前序遍历右子树。
def preorder(tree):
if tree:
print(tree.getRootVal())
preorder(tree.getLeftChild())
preorder(tree.getRightChild())
也可以在BinaryTree类里写一个方法,一般情况下,只需要用self取代tree,但是还要修改基点。内部方法必须检查左右孩子是否存在。
def preorder(self):
print(self.key)
if self.leftChild:
self.leftChild.preorder()
if self.rightChild:
self.rightChild.preorder()
在这里, preorder 作为一个外部函数比较好,原因是,我们很少是为了遍历而遍历,这个过程中总是要做点操作的。
3.2 中序遍历
在中序遍历中,先递归中序遍历左子树,然后访问根节点,最后递归中序遍历右子树。
def inorder(tree):
if tree:
inorder(tree.getLeftChild())
print(tree.getRootVal())
inorder(tree.getRightChild())
3.3 后序遍历
在后序遍历中,先递归后序遍历左子树,然后是右子树,最后是根节点。
def postorder(tree):
if tree:
preorder(tree.getLeftChild())
preorder(tree.getRightChild())
print(tree.getRootVal())
3.4 遍历代码测试
preorder(r)
#root!
#leftTree!
#new_rightTree!
inorder(r)
#leftTree!
#root!
#new_rightTree!
postorder(r)
#leftTree!
#new_rightTree!
#root!
#------------------
r.preorder()
#root!
#leftTree!
#new_rightTree!
4 分析树(ADT)
分析树主要用于真实世界的结构表示,象语法或数学表达式等。比如((7+3)∗(5−2))的分析树如下:
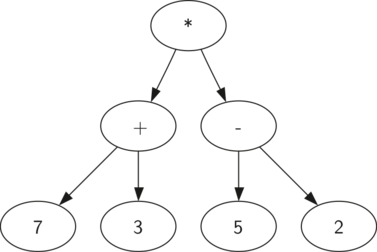
4.1 数学表达式分析树构建规则
构建分析树,第一步是把表达式分解成符号保存在列表里。这里面有4种符号:左括号,右括号,操作符,操作数。我们知道每当读到一个左括号,就是新开一个表达式,这时就要新建一个子树来对应括号内的表达式。相反地,每读到一个右括号,这个子表达式就结束了。另外我们也要知道,操作数总是操作符的叶子。最后我们要知道,每个操作符都有左右两个孩子。知道了以上信息,我们可以给出以下规则:
- 如果当前符号是
(,新增一个节点作为当前节点的左孩子,并下沉到这个左孩子。 - 如果当前符号在
['+','-','/','*'],把当前节点的值赋为当前符号,并且为当前节点增加一个右孩子,并下沉到这个右孩子。 - 如果当前符号是一个数字,把当前节点值设为这个数,返回到父母节点。
- 如果当前符号是
),返回到父母节点。
我们必须保持对“当前节点”和它的“父母节点”的跟踪。树的接口已经提供了获得孩子节点的方法,getLeftChild和getRightChild但是怎样跟踪父母呢?一个简单方法就是使用栈,每当下沉到当前节点的孩子时,先把当前节点压栈,当要返回到当前节点的父母时,从栈中弹出。
使用以上规则,加上Stack和BinaryTree的操作,分析树的代码实现如下:
from pythonds.basic.stack import Stack
from pythonds.trees.binaryTree import BinaryTree
import operator
def buildParseTree(fpexp):
fplist = fpexp.split()
pStack = Stack()
eTree = BinaryTree('') # -------------------------------建
pStack.push(eTree) # -----------------------------------压(记录)
currentTree = eTree # ----------------------------------设(下沉)
for i in fplist:
# 如果当前符号是’(‘,新增一个节点作为当前节点的左孩子,并下沉到这个左孩子
if i == '(':
currentTree.insertLeft('') # -------------------建
pStack.push(currentTree) # ---------------------压(记录)
currentTree = currentTree.getLeftChild() # -----设(下沉)
# 如果当前符号是一个数字,把当前节点值设为这个数,返回到父母节点。
elif i not in ['+', '-', '*', '/', ')']:
currentTree.setRootVal(int(i)) # ---------------写
currentTree = pStack.pop() # -------------------排、设(上浮)
# 如果当前符号在 ['+','-','/','*'],把当前节点的值赋为当前符号
# 并且为当前节点增加一个右孩子,并下沉到这个右孩子
elif i in ['+', '-', '*', '/']:
currentTree.setRootVal(i) # --------------------写
currentTree.insertRight('') # ------------------建
pStack.push(currentTree) # ---------------------压(记录)
currentTree = currentTree.getRightChild() # ----设(下沉)
# 如果当前符号是‘)’, 返回到父母节点
elif i == ')':
currentTree = pStack.pop() # -------------------排、设(上浮)
else:
raise ValueError
return eTree
4.2 分析树求值
我们写一个函数来求分析树的值,返回计算结果。写这个函数要用到树的层级结构,我们写一个递归算法对子树求值。
我们从设计递归的基点开始。树的自然基点是叶子。在分析树中,叶子节点总是操作数,象整数或浮点数之类的数字对象不需要更多操作,所以evaluate函数可以直接返回它的值。递归走向基点的的方法是对左右孩子使用evaluate函数。要把两个递归调用的结果合在一起,只需要简单地对这两个结果应用存在父母节点的操作符。
#后序遍历版本:
def evaluate(parseTree):
opers = {'+': operator.add, '-': operator.sub, '*': operator.mul, '/': operator.truediv}
leftC = parseTree.getLeftChild()
rightC = parseTree.getRightChild()
# 分析树求值,是后序遍历的一个普通用法:计算左右子树的值,然后用操作函数结合在一起
if leftC and rightC:
fn = opers[parseTree.getRootVal()]
return fn(evaluate(leftC), evaluate(rightC))
else:
return parseTree.getRootVal()
def postordereval(tree):
opers = {'+': operator.add, '-': operator.sub, '*': operator.mul, '/': operator.truediv}
res1 = None
res2 = None
if tree:
res1 = postordereval(tree.getLeftChild())
res2 = postordereval(tree.getRightChild())
if res1 and res2:
return opers[tree.getRootVal()](res1, res2)
else:
return tree.getRootVal()