Classic sort
01 Oct 2016先上结果
- 插入排序
def insertionSort1(L):
for i in range(1, len(L)):
curV = L[i]
pos = i
while pos > 0 and curV < L[pos - 1]:
L[pos] = L[pos - 1]
pos -= 1
L[pos] = curV #找到正确的位置插入
return L
- 冒泡排序
def shortBubbleSort(L):
exchanges = True
passnum = len(L) - 1
while passnum > 0 and exchanges:
exchanges = False # 若标记出该轮没有逆序,则冒泡排序就可以提前停止
for i in range(passnum):
if L[i] > L[i + 1]:
exchanges = True
L[i], L[i + 1] = L[i + 1], L[i]
passnum -= 1
- 二分归并排序
def mergeSort(L, start, end):
if (end - start) < 2:
return L
mid = (start + end) // 2
L = mergeSort(L, start, mid)
L = mergeSort(L, mid, end)
temp_L = L[start: mid]
local = 0
while local < len(temp_L): # 不同于start<end,因为相对而言,后者复杂度更高
if mid >= end or temp_L[local] <= L[mid]:
L[start] = temp_L[local]
local += 1
else:
L[start] = L[mid]
mid += 1
start += 1
return L#将排好序的list返回,供上一层的递归使用
L = list(range(8, 0, -1))
mergeSort(L, 0, 8)
- 快速排序
def quickSort(L, begin, end):
if begin < end:
pivot = L[begin]
i = begin
for j in range(begin + 1, end + 1):
if L[j] < pivot:
i += 1
L[i], L[j] = L[j], L[i]
L[begin], L[i] = L[i], L[begin]
quickSort(L, begin, i - 1)
quickSort(L, i + 1, end)
return L
- 堆排序
def heap_sort(elems, e, begin, end):
def siftDown(elems, e, begin, end):
i, j = begin, begin * 2 + 1
while j < end:
if j + 1 < end and elems[j + 1] < elems[j]:
j += 1
if e < elems[j]:
break
elems[i] = elems[j]
i, j = j, j * 2 + 1
elems[i] = e
end = len(elems)
for i in range(end // 2, -1, -1):
siftDown(elems, elems[i], i, end)
for i in range((end - 1), 0, -1):
e = elems[i]
elems[i] = elems[0]
siftDown(elems, e, 0, i)
冒泡排序
简介
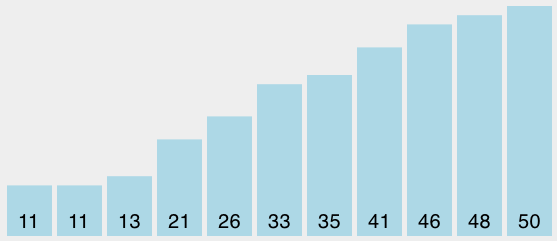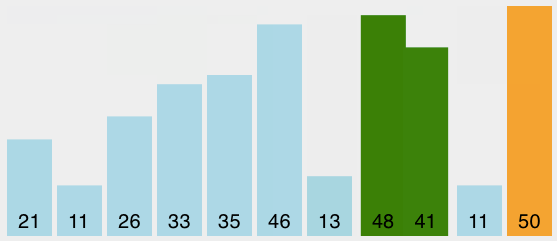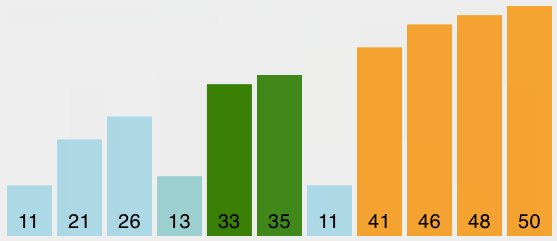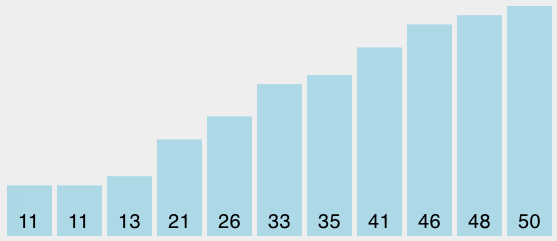
冒泡排序是一种典型的(也是最简单的)通过反复比较交换元素来消除逆序,实现排序的方法。冒泡排序方法需要多次访问列表,它比较相邻的两个元素,如果次序不对,就交换位置。每次遍历就象气泡上浮到合适的位置一样,把经历的最大的元素放到合适的位置上。 普通冒泡排序的python代码如下:
def BubbleSort(alist):
for i in range(len(alist) - 1): # 一共需要进行 n-1 轮比较交换
for j in range(1, len(alist) - i): # 在第 i 轮中,需要进行 n-i 次比较
if alist[j - 1] > alist[j]:
alist[j - 1], alist[j] = alist[j], alist[j - 1]
print('第%s轮'%(i+1),alist)
alist = [21, 46, 33, 11, 26, 50, 35, 48, 13, 41, 11]
BubbleSort(alist)
# 排序过程如下:
# 初始状态 [21, 46, 33, 11, 26, 50, 35, 48, 13, 41, 11]
# 第1轮过后 [21, 33, 11, 26, 46, 35, 48, 13, 41, 11, 50]
# 第2轮过后 [21, 11, 26, 33, 35, 46, 13, 41, 11, 48, 50]
# 第3轮过后 [11, 21, 26, 33, 35, 13, 41, 11, 46, 48, 50]
# 第4轮过后 [11, 21, 26, 33, 13, 35, 11, 41, 46, 48, 50]
# 第5轮过后 [11, 21, 26, 13, 33, 11, 35, 41, 46, 48, 50]
# 第6轮过后 [11, 21, 13, 26, 11, 33, 35, 41, 46, 48, 50]
# 第7轮过后 [11, 13, 21, 11, 26, 33, 35, 41, 46, 48, 50]
# 第8轮过后 [11, 13, 11, 21, 26, 33, 35, 41, 46, 48, 50]
# 第9轮过后 [11, 11, 13, 21, 26, 33, 35, 41, 46, 48, 50]
# 第10轮过后 [11, 11, 13, 21, 26, 33, 35, 41, 46, 48, 50]
特点与不足
观察上面的代码运行过程可知,之所以每次能保证把最大的元素排到正确的位置,是由于需要的list左小右大,并且以从左至右的方向来访问排序的缘故。若是以从右至左的方向来访问排序,则能保证把最小的元素排到正确的位置上。所以其特点总结如下:
***
- 每一轮检查可以把一个最大元素交换到位,一些较大元素向右移动一段距离,可以移动很远。
- 因为采用从左至右的顺序来比较,导致小元素一次只能左移一位。若list中的小元素距离目标位置很远(既位置很靠右),可能会延误整个排序过程。
改进 1
虽然有时冒泡排序确实需要进行n-1轮比较交换,但那是最小元素恰好在最右时的特例。在其他的情形,扫描就不需要进行那么多轮。若发现排序已经完成,就不需要进行n-1轮比较交换,可以提前结束排序过程。以此来改进的算法通常称为短冒泡算法,代码如下:
def shortBubbleSort(alist):
exchanges = True
passnum = len(alist) - 1
while passnum > 0 and exchanges:
exchanges = False # 若标记出该轮没有逆序,则冒泡排序就可以提前停止
for i in range(passnum):
if alist[i] > alist[i + 1]:
exchanges = True
alist[i], alist[i + 1] = alist[i + 1], alist[i]
passnum -= 1
print('第%s轮过后' % (len(alist) - passnum - 1), alist)
alist = [21, 46, 11, 33, 11, 26, 50, 35, 48, 13, 41]
shortBubbleSort(alist)
# 排序过程如下:
# 初始状态 [21, 46, 11, 33, 11, 26, 50, 35, 48, 13, 41]
# 第1轮过后 [21, 11, 33, 11, 26, 46, 35, 48, 13, 41, 50]
# 第2轮过后 [11, 21, 11, 26, 33, 35, 46, 13, 41, 48, 50]
# 第3轮过后 [11, 11, 21, 26, 33, 35, 13, 41, 46, 48, 50]
# 第4轮过后 [11, 11, 21, 26, 33, 13, 35, 41, 46, 48, 50]
# 第5轮过后 [11, 11, 21, 26, 13, 33, 35, 41, 46, 48, 50]
# 第6轮过后 [11, 11, 21, 13, 26, 33, 35, 41, 46, 48, 50]
# 第7轮过后 [11, 11, 13, 21, 26, 33, 35, 41, 46, 48, 50]
# 第8轮过后 [11, 11, 13, 21, 26, 33, 35, 41, 46, 48, 50]
# 第8轮发现排序已经完成, 就不再进行比较交换操作, 所以结果和第七轮结果一致
时间复杂度
一般认为冒泡排序是效率最差的排序方法,因为它在元素最终确定位置之前反复交换。这些浪费的交换操作很费资源。冒泡排序的性质很清楚:最坏的情况(每次比较都引发一次交换),及最好的情况下(如果列表是有序的,一次交换也没有),时间复杂度都是O(n^2)。
改进 2
冒泡排序的低效率,究其原因,有以下两个方面:
***
- 反复交换中,做的赋值操作较多,累积起来的代价也较大。
- 距离最终位置很远的元素拉低了整个算法的效率。
其中,为了解决上述的第二个问题,我们可以采用快速排序算法。 另一种简单的解决方法是交错冒泡排序:从左至右、从右至左,这两种比较交换的顺序交替进行,以便把小元素快速移向左方(从右至左的时候)。以此来改进的算法通常称为交替冒泡算法,代码如下:
def interlaceBubbleSort(alist):
exchanges = True
first = 1
last = len(alist)
positive = True
for i in range(last - 1): # 一共需要进行 n-1 轮比较交换
exchanges = False
if positive == True:
for j in range(first, last): # 在第 i 轮中,需要进行 n-i 次比较
if alist[j - 1] > alist[j]:
exchanges = True
alist[j - 1], alist[j] = alist[j], alist[j - 1]
first -= 1
last -= 2
positive = not positive
else:
for j in range(last, first, -1): # 在第 i 轮中,需要进行 n-i 次比较
if alist[j - 1] > alist[j]:
exchanges = True
alist[j - 1], alist[j] = alist[j], alist[j - 1]
first += 2
last += 1
positive = not positive
if exchanges == False:
break
alist = [21, 46, 33, 11, 26, 50, 35, 48, 13, 41, 11]
interlaceBubbleSort(alist)
# 排序过程如下:
# 初始状态 [21, 46, 33, 11, 26, 50, 35, 48, 13, 41, 11]
# 第1轮过后 [21, 33, 11, 26, 46, 35, 48, 13, 41, 11, 50]
# 第2轮过后 [11, 21, 33, 11, 26, 46, 35, 48, 13, 41, 50]
# 第3轮过后 [11, 21, 11, 26, 33, 35, 46, 13, 41, 48, 50]
# 第4轮过后 [11, 11, 21, 13, 26, 33, 35, 46, 41, 48, 50]
# 第5轮过后 [11, 11, 13, 21, 26, 33, 35, 41, 46, 48, 50]
总结
针对两种改进方式,我进行了运行时间的计算实验,在ipython环境下的实验代码及结果如下:
alist = [21, 46, 33, 11, 26, 50, 35, 48, 13, 41, 11]
print('BubbleSort:')
%timeit BubbleSort(alist)
print('shortBubbleSort:')
%timeit shortBubbleSort(alist)
print('interlaceBubbleSort:')
%timeit interlaceBubbleSort(alist)
#结果:
BubbleSort:
100000 loops, best of 3: 12.1 µs per loop
shortBubbleSort:
1000000 loops, best of 3: 1.92 µs per loop
interlaceBubbleSort:
100000 loops, best of 3: 2.6 µs per loop
观察可见,交错算法的改进效果并没有像想象中的那样比短冒泡排序的效果更好。在加大数列的长度到几百时,效果也仅仅略微优于短冒泡排序。我觉得应该是我的算法实现的过于复杂,应该有更为精简的程序,可以达到理想中的效果。
选择排序
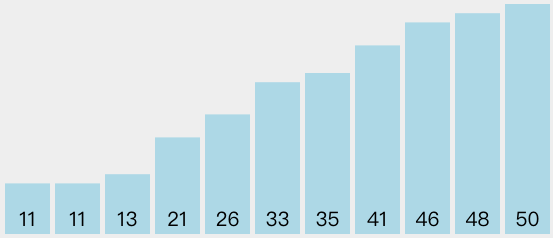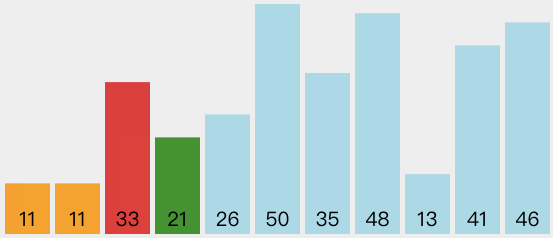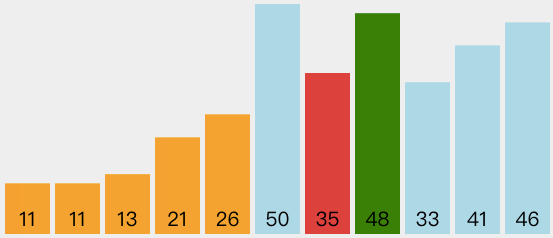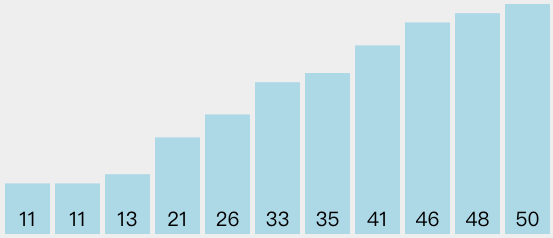
简介
选择排序是冒泡排序的改进,一次遍历只做一次交换。它在一次遍历中找到最大的元素,结束时放到合适的位置,正如冒泡排序一样,一次遍历后最大的元素就位。第二次遍历后,第二小的元素就位,这样持续进行,需要n-1个遍历来为n个元素排序。
代码实现
def selectionHeavySort(alist):
for i in range(len(alist), 1, -1):
positionOfMax = 0
for j in range(1, i):
if alist[positionOfMax] < alist[j]:
positionOfMax = j
alist[positionOfMax], alist[i - 1] = alist[i - 1], alist[positionOfMax]
alist = [21, 46, 33, 11, 26, 50, 35, 48, 13, 41, 11]
selectionHeavySort(alist)
print(alist)
另一种实现方式
也可以在每次遍历中寻找最小的元素,找到后放在合适的位置上,然后下一轮遍历结束后,大小排第二的元素就位,这样持续进行,同样需要n-1个遍历来为n个元素排序。
def selectionLightSort(alist):
for i in range(len(alist)):
positionOfMin = i
for j in range(i+1, len(alist)):
if alist[positionOfMin] > alist[j]:
positionOfMin = j
alist[positionOfMin], alist[i] = alist[i], alist[positionOfMin]
alist = [21, 46, 33, 11, 26, 50, 35, 48, 13, 41, 11]
selectionLightSort(alist)
print(alist)
可以看出,选择排序和冒泡排序一样多的比较次数,所以它的性能依然是O(n^2)。不过,因为交换次数的减少,选择排序一般运行得比冒泡要快。
插入排序
1 简介
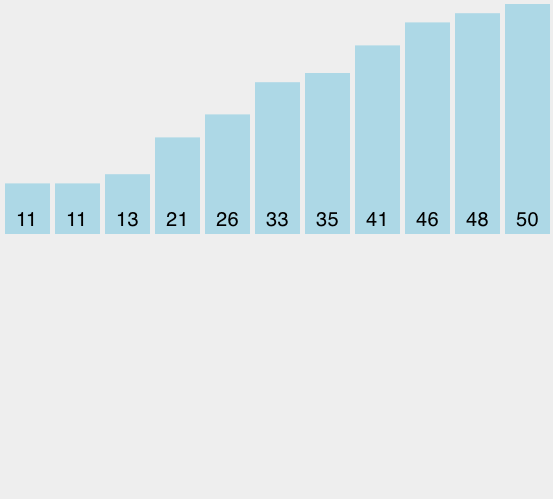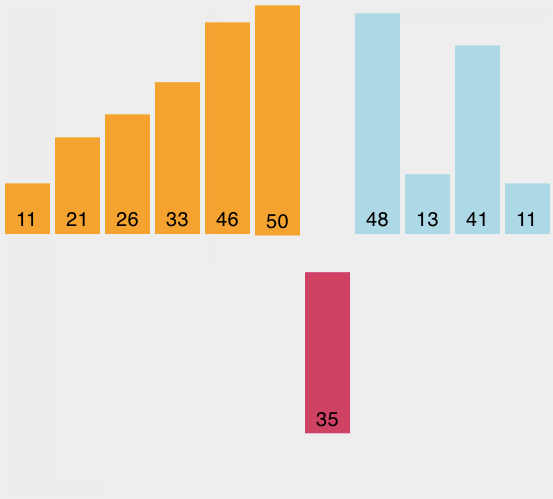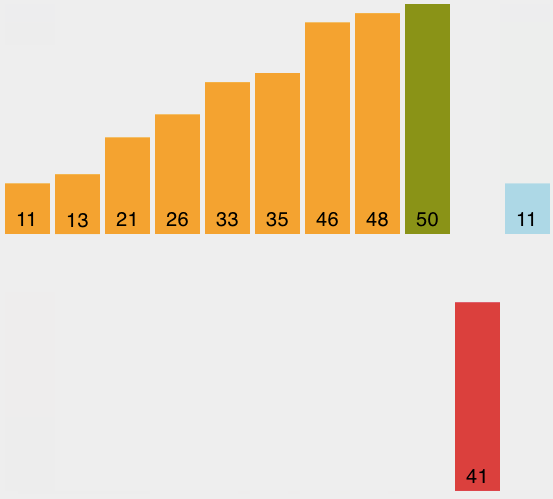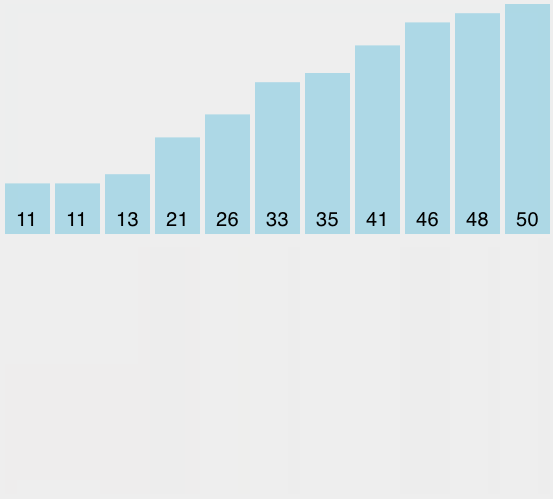
插入排序虽然仍然是O(n^2),但工作模式就有稍微不同。它总是在列表的低端保持一个有序的子列表,后面的元素被逐个“插入”到前面的有序子表,这样有序的子表就逐渐变大。图4是插入排序的过程,阴影部分是排好序的子列表。
开始的时候我们假设一个只有一个元素(在0位上)的列表而且是有序的,每次遍历的时候,从1到n-1的每个元素,与有序的子列表进行比较。当回顾已经排序的子表时候,比当前元素大的向前移,当遇到一个比它小的元素或到达子表的终点时,当前元素就插在这个位置上。
2 代码实现
实现的时关于循环语句一点细节体会,while相较于for:
优点:while可以在循环语句的地方进行条件判断结束时机,而for需要内部写if、break来判断,不优雅。缺点:while计数的话需要单独写一个变量自增或自减,而if的变量增减是自动进行的,虽然底层实现都一样,但是后者更优雅。
def insertionSort1(alist):
for i in range(1, len(alist)):
currentvalue = alist[i]
position = i
# while相较于for的 优点 是可以在循环语句的地方进行条件判断,而for需要内部写if来break
# while相较于for的 缺点 是计数的话需要单独写一个变量
while position > 0 and currentvalue < alist[position - 1]:
alist[position] = alist[position - 1]
position -= 1
alist[position] = currentvalue
return alist
#以下是用for来写的形式,实现原理同上面是一样的
def insertionSort2(alist):
for i in range(1, len(alist)):
currentvalue = alist[i]
for j in range(i, -1, -1):
# 同样需要两个判断条件
if currentvalue < alist[j - 1] and j > 0:
alist[j] = alist[j - 1]
else:
alist[j] = currentvalue
break
return alist
值得一提的是,我又利用python自带的list数据结构的方法(可以使用pop和insert)实现了该排序,不过算法细节上不同之处是,每一轮插入,没有将元素一个个的对比左移,而是直接从开头向右一个个移动,对比插入,这样的好处是可以不写else分支,充分利用pop和insert方法,使语句最简化。虽然简洁,但相较于上面的insertionSort1 ,该实现方式性能很差,这大概也是python高简洁、低性能的体现:
def insertionSort3(alist):
for i in range(1, len(alist)):
for j in range(i):
if alist[i] <= alist[j]:
# 用了python自带的数据结构方法实现,虽然看上去更为简洁,但性能很差
alist.insert(j, alist.pop(i))
return alist
此处的时间复杂度性能仍有待深入讨论,文中内容待考证
3 性能测试
利用ipython的环境来对上面3个函数进行时间上的性能测试:
import random
alist3=alist2[:]=alist1[:]=random.sample(range(100), 100)
print('insertionSort1:')
%timeit insertionSort1(alist1)
print('insertionSort2:')
%timeit insertionSort2(alist2)
print('insertionSort3:')
%timeit insertionSort3(alist3)
#测试结果如下:
insertionSort1:
The slowest run took 24.02 times longer than the fastest. This could mean that an intermediate result is being cached.
10000 loops, best of 3: 20.7 µs per loop
insertionSort2:
The slowest run took 7.40 times longer than the fastest. This could mean that an intermediate result is being cached.
10000 loops, best of 3: 63.3 µs per loop
insertionSort3:
1000 loops, best of 3: 468 µs per loop
经过以上测试可知,利用最基本的语法实现的插入排序算法,性能最优。
Ps.总结一下,实现生成随机整数list的方式:
- 允许元素重复:
[radom.randint(a,b) for i in range(c,d)] - 不允许元素重复:
random.sample(range(a,b),c)
希尔排序
1 简介
希尔排序,有时称为递减增量排序,是在插入排序基础上,把列表拆成几个较小的子表,然后对每个子表使用插入排序的方法。选出子表的方法是希尔排序的关键,它并不是把列表的中相近的元素取出来组成子表,而是使用了一个增量值I,有时也叫做“间隔”,然后每隔一个间隔选中一个元素来组成子表。每个子表单独做插入排序。完成之后虽然没有完全排序,但对子表排序后,元素已经很接近它们的最终位置。
2 代码实现
def shellSort(alist):
sublistcount = len(alist) // 2
while sublistcount > 0:
for startposition in range(sublistcount):
gapInsertionSort(alist, startposition, sublistcount)
print('After increments of size', sublistcount, 'The list is', alist)
sublistcount = sublistcount // 2
print('\nFinish:', alist)
#这里用到的是以一定间隔为跨度的插入排序:
def gapInsertionSort(alist, start, gap):
for i in range(start, len(alist), gap):
currentvalue = alist[i]
position = i
while position >= gap and currentvalue < alist[position - gap]:
alist[position] = alist[position - gap]
position -= gap
alist[position] = currentvalue
3 算法性能
乍看起来,希尔排序不见得比插入排序更好,因为最后一步就完全是一个插入排序。但是,最后一步的插入排序,不需要很多步骤来完成比较和移动,因为通过前面的增量插入排序,列表已经做了“预排序”,也就是说,这个列表已经比普通列表“更有序”,所以在效率上有很大的不同。
本文不对希尔排序的时间性能进行详细分析,不过我们可以说,它趋向于O(n)和O(n^2)之间。对于上面代码中的增量,性能是O(n^2),变更增量,例如使用2k−1(1, 3, 7,15, 31等),性能可达到O(n^(3/2))。
归并排序
1 简介
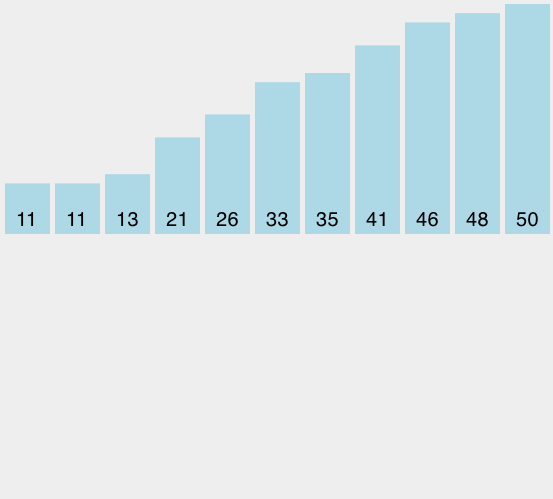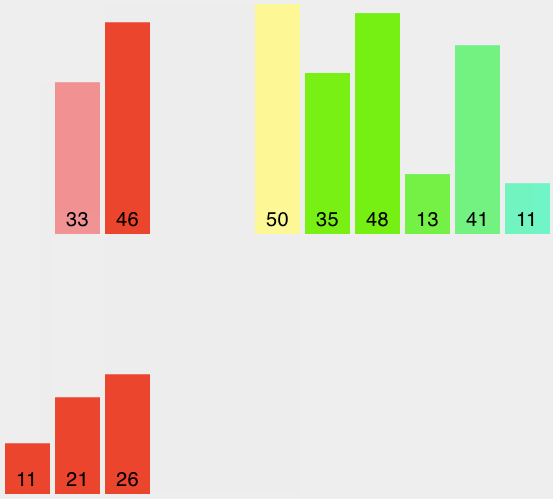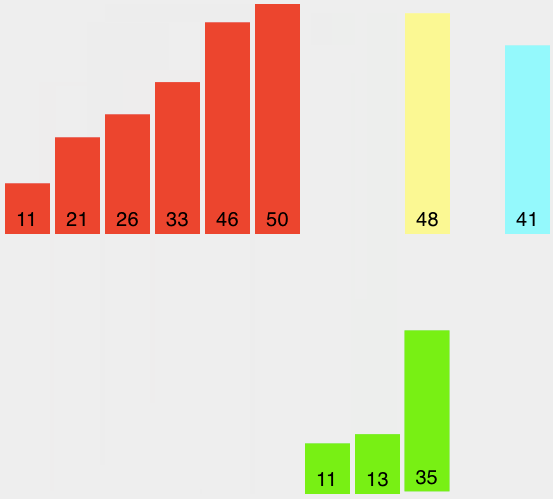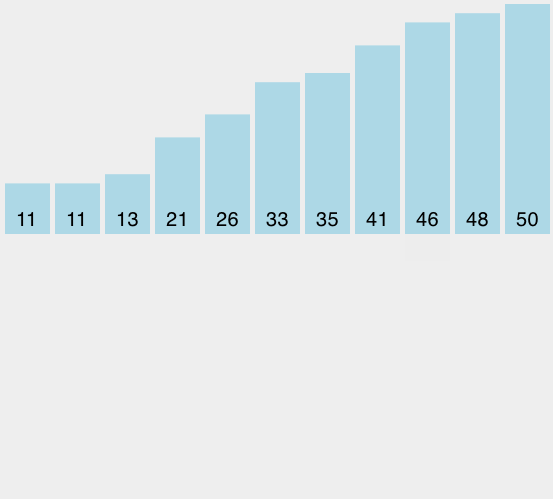
在提高排序算法性能的方法中,有一类叫做分而治之。我们先研究其中第一种叫做归并排序。归并排序使用递归的方法,不停地把列表一分为二。如果列表是空或只有一个元素,那么就是排好序的(递归基点),如果列表有超过1个的元素,那么切分列表并对两个子列表递归使用归并排序。一旦这两个列表排序完成,称为“归并”的基本操作开始执行。归并是把两个有序列表合并成一个新的有序列表的过程。
2 算法实现
函数开始查询基点,如果列表长度小于等于1,那么已经是有序的不需要进一步处理,否则,长度大于1,就要用列表的切片操作分拆成左半部和右半部。注意列表的元素数量未必是个偶数,那没关系,长度相关最大也不超过1个。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
__author__ = 'Fu Yangzhen'
# Created on 2016/9/25
def mergeSort(alist):
print('Splitting', alist)
if len(alist) > 1: # 递归结束的判断条件
mid = len(alist) // 2
leftHalf = alist[:mid]
rightHalf = alist[mid:]
mergeSort(leftHalf)
mergeSort(rightHalf)
i = 0
j = 0
k = 0
while i < len(leftHalf) and j < len(rightHalf): # 循环条件保证可以遍历完至少一个Half
if leftHalf[i] < rightHalf[j]:
alist[k] = leftHalf[i]
i += 1
else:
alist[k] = rightHalf[j]
j += 1
k += 1
while i < len(leftHalf): # 若还有没遍历完的Half,就继续遍历
alist[k] = leftHalf[i] # 不需要再进行比较,因为只会多出一个最大的元素未排入alist
i += 1
k += 1
while j < len(rightHalf): # 右半边同理
alist[k] = rightHalf[j]
j += 1
k += 1
print('Merging', alist)
alist = [21, 46, 33, 11, 26, 50, 35, 48, 13, 41, 11]
mergeSort(alist)
print(alist)
程序运行结果如下:
Splitting [21, 46, 33, 11, 26, 50, 35, 48, 13, 41, 11]
Splitting [21, 46, 33, 11, 26]
Splitting [21, 46]
Splitting [21]
Merging [21]
Splitting [46]
Merging [46]
Merging [21, 46]
Splitting [33, 11, 26]
Splitting [33]
Merging [33]
Splitting [11, 26]
Splitting [11]
Merging [11]
Splitting [26]
Merging [26]
Merging [11, 26]
Merging [11, 26, 33]
Merging [11, 21, 26, 33, 46]
Splitting [50, 35, 48, 13, 41, 11]
Splitting [50, 35, 48]
Splitting [50]
Merging [50]
Splitting [35, 48]
Splitting [35]
Merging [35]
Splitting [48]
Merging [48]
Merging [35, 48]
Merging [35, 48, 50]
Splitting [13, 41, 11]
Splitting [13]
Merging [13]
Splitting [41, 11]
Splitting [41]
Merging [41]
Splitting [11]
Merging [11]
Merging [11, 41]
Merging [11, 13, 41]
Merging [11, 13, 35, 41, 48, 50]
Merging [11, 11, 13, 21, 26, 33, 35, 41, 46, 48, 50]
[11, 11, 13, 21, 26, 33, 35, 41, 46, 48, 50]
3 性能分析
要分析mergeSort函数,需要考虑函数中两个分立的过程。第一个,把列表一分为二,我们已经在二分查找中计算过了,对于长为n的列表,需要logn的时间来切分。第二个是归并过程。列表中每个元素都要被处理并放在有序表中,所有归并操作n个元素的列表,需要n步操作。这样结果就是,logn步操作,每步操作包括n步归并,所以最终为nlogn。
要注意的是,mergeSort函数需要额外的内存来保存切出的两个子表,当数据集很大时,问题会变得很严重。
回想列表切片的操作,如果切片大小是k,那么这个操作的性能是O(k),为了保证mergeSort的性能是O(nlogn) ,我们需要清除切片操作。这样,我们需要简单地将开始和结束的索引值连同列表一起传递给递归过程:
def mergeSort(alist,start,end):
print('Splitting', alist[start:end+1])
if end>start:
mid = (end-start+1) // 2
leftHalfEnd = start+mid-1
rightHalfStart = start+mid
mergeSort(alist,start,leftHalfEnd)
mergeSort(alist,rightHalfStart,end)
i = start
j = rightHalfStart
k = 0
tempList=[None]*(end-start+1)
while i <= leftHalfEnd and j <= end: # 循环条件保证可以遍历完至少一个Half
if alist[i] < alist[j]:
tempList[k] = alist[i]
i += 1
else:
tempList[k] = alist[j]
j += 1
k += 1
while i <= leftHalfEnd: # 若还有没遍历完的Half,就继续遍历
tempList[k] = alist[i] # 不需要再进行比较,因为只会多出一个最大的元素未排入alist
i += 1
k += 1
while j <= end: # 右半边同理
tempList[k] = alist[j]
j += 1
k += 1
while k >=1:
alist[start+k-1]=tempList[k-1]
k-=1
print('Merging', alist[start:end+1])
alist = [21, 46, 33, 11, 26, 50, 35, 48, 13, 41, 11]
mergeSort(alist,0,len(alist)-1)
print(alist)
这里虽然传递了列表的索引来进行递归,免去了切片操作,但是在归并的操作中,还是利用了一个中间列表
tempList来储存排序结果,并在排序后逐个地替换原表的数值,这其实还是增加了时间复杂度,实在是想不到有更好的方法来高效地进行排序操作……
3.1 最优版本
下面是墨灵大哥写的申请内存最小的版本,每次申请空间都只有要排序的1/2。优化的关键点是,递归之前别用切片来截半,切片是要申请内存的行为(排序的时候借助temp list的动作是无法避免的,temp list只用排序list的一半长度是极限方法了),要尽可能地减少这个操作:
def mergeSort(L, start, end):
if (end - start) < 2:
return L
mid = (start + end) // 2
L = mergeSort(L, start, mid)
L = mergeSort(L, mid, end)
temp_L = L[start: mid]
local = 0
while local < len(temp_L): # 不同于start<end,因为相对而言,后者复杂度更高
if mid >= end or temp_L[local] <= L[mid]:
L[start] = temp_L[local]
local += 1
else:
L[start] = L[mid]
mid += 1
start += 1
print(L)
return L#将排好序的list返回,供上一层的递归使用
L = list(range(8, 0, -1))
mergeSort(L, 0, 8)
快速排序
1 简介
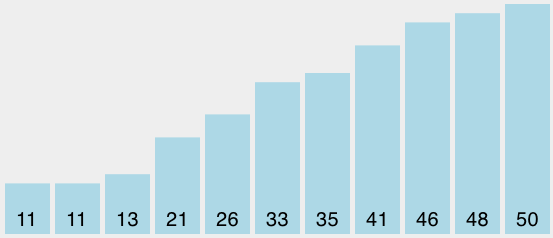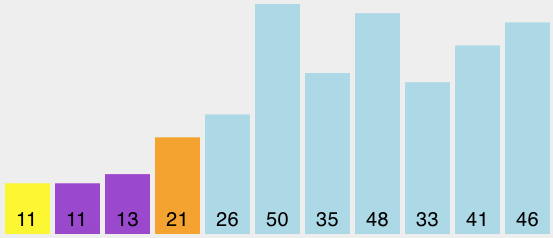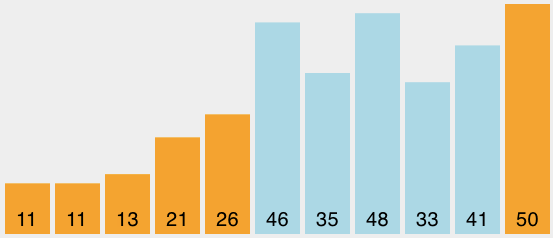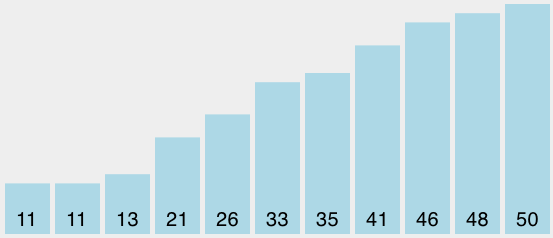
快速排序也使用了分而治之的策略来提高性能,而且不需要额外的内存,但是这么做的代价就是,列表不是对半切分的,因而,性能上就有所下降。 快速排序选择一个数值,一般称为“轴点”,虽然有很多选取轴点的方法,我们还是简单地把列表中第一个元素做为轴点了。轴点的作用是帮助把列表分为两个部分。列表完成后,轴点所在的位置叫做“切分点”,从这一点上把列表分成两部分供后续调用。
2 算法实现
2.1 一般方式实现
def quickSort(L, begin, end):
if begin < end:
pivot = L[begin]
leftMark = begin + 1
rightMark = end
while leftMark <= rightMark:
while leftMark <= rightMark and L[leftMark] <= pivot:
leftMark += 1
while leftMark <= rightMark and L[rightMark] >= pivot:
rightMark -= 1
if leftMark < rightMark: # lM和rM如果交错或者对齐了的话,就没必要互相交换了
L[rightMark], L[leftMark] = L[leftMark], L[rightMark]
L[rightMark], L[begin] = L[begin], L[rightMark]
quickSort(L, begin, rightMark - 1)
quickSort(L, rightMark + 1, end)
return L
2.2 另一种简单实现
def quickSort2(L, begin, end):
if begin < end:
pivot = L[begin]
i = begin
for j in range(begin + 1, end + 1):
if L[j] < pivot:
i += 1
L[i], L[j] = L[j], L[i]
L[begin], L[i] = L[i], L[begin]
quickSort2(L, begin, i - 1)
quickSort2(L, i + 1, end)
return L
3 性能分析
为了分析快速排序函数性能,要注意到一个长度为n的列表,如果切分点总是在列表的中间,那么就是要logn次切分。为了找到切分点,n个元素都要与轴点作一次比较,结果需要nlogn。另外,也不需要象归并排序一样消耗额外的内存。不幸的是,在最怀的情况下,切分点不在中间,而是偏左或偏右,生成很不均匀的子表,这种情况下,生成的子表是一个0个元素,一个n-1个元素,然后再切分,却生成一个子表是0个元素,另一个是n-2个元素等等。结果需要的开销就是O(n^2)。