Decision tree - ID3
17 Sep 20161 简介
ID3算法(Iterative Dichotomiser 3 迭代二叉树3代)是一个由Ross Quinlan发明的用于决策树的算法。
这个算法是建立在奥卡姆剃刀的基础上:越是小型的决策树越优于大的决策树(简单理论)。尽管如此,该算法也不是总是生成最小的树形结构。而是一个启发式算法。奥卡姆剃刀阐述了一个信息熵的概念:

这个ID3算法可以归纳为以下几点:
- 使用所有没有使用的属性并计算与之相关的样本熵值
- 选取其中熵值最小的属性
- 生成包含该属性的节点
还有其他决策树的构造算法,最流行的是CART和C4.5。关于ID3算法的实现可以参考C4.5算法,它同时也是ID3的升级版。
以上介绍来自维基百科。
2 代码实现
源码来自[<机器学习实战>](https://book.douban.com/subject/24703171/)ch03,本文对其进行必要的整理、注释及修订。
2.1 计算信息熵
信息熵计算函数:
#=======================================================================计算信息熵
from math import log
def calcShannonEnt(dataSet):
numEntries=len(dataSet)
labelCounts={}
for featVec in dataSet:
currentLabel=featVec[-1]
labelCounts[currentLabel]=labelCounts.get(currentLabel,0)+1
shannonEnt=0.0
for key in labelCounts:
prob=float(labelCounts[key])/numEntries
shannonEnt-=prob*log(prob,2)
return shannonEnt
测试信息熵计算函数:
#================================================================测试用数据生成函数
def createDataSet():
dataSet=[[1,1,'yes'],
[1,1,'yes'],
[1,0,'no'],
[0,1,'no'],
[0,1,'no']]
labels=['no surfacing','flippers']
return dataSet,labels
myDat,labels=createDataSet()
calcShannonEnt(myDat)#0.9709505944546686
2.2 选择最好的数据集划分方式
按照指定的特征索引划分样本:
#=============================================================按照指定特征划分数据集
def splitDataSet(dataSet,axis,value):
retDataSet=[]
for featVec in dataSet:
if featVec[axis]==value:
readucedFeatVec=featVec[:axis]
readucedFeatVec.extend(featVec[axis+1:])
retDataSet.append(readucedFeatVec)
return retDataSet
splitDataSet(myDat,0,1)#[[1, 'yes'], [1, 'yes'], [0, 'no']]
选出在当前样本集的各个特征中能最使初始的信息增益达到最高的那个特征:
#===========================================================选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
numFeatures=len(dataSet[0])-1
baseEntropy=calcShannonEnt(dataSet)
baseInfoGain=0.0;bestFeature=-1
for i in range(numFeatures):
featList=[example[i] for example in dataSet]
uniqueVals=set(featList)#Ps.从列表创建集合是python中得到列表唯一元素的 最快方法
newEntropy=0.0
for value in uniqueVals:
subDatSet=splitDataSet(dataSet,i,value)
prob=len(subDatSet)/float(len(dataSet))
newEntropy+=prob*calcShannonEnt(subDatSet)
infoGain=baseEntropy-newEntropy
if infoGain>baseInfoGain:#信息增益是熵的减少,即数据无序度的减少。减少得越多越好
baseInfoGain=infoGain
bestFeature=i
return bestFeature
2.3 递归构建决策树
#===================================================================递归构建决策树
import operator
def majorityCnt(classList):#各类型的样本都有时,个数多的决定当前样本集的类型
classCount={}
for vote in classList:
classCount[vote]=classList.get(vote,0)+1
sortedClassCount=sorted(classCount.items(),
key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
def createTree(dataSet,labels):
classList=[example[-1] for example in dataSet]#收集当前的class种类名称
if len(set(classList))==1:#只有一个种类时,就返回该种类名称,停止递归
return classList[0]
if len(dataSet[0])==1:#遍历完所有的特征了,只剩下class列,返回最多的种类名字,停止递归
return majorityCnt(classList)
bestFeat=chooseBestFeatureToSplit(dataSet)#先找到信息增益最优的特征
bestFeatLabel=labels[bestFeat]#该最优特征的名字
myTree={bestFeatLabel:{}}#以此特征来划分
del(labels[bestFeat])
featValues=[example[bestFeat] for example in dataSet]#收集所有样本该特征对应的数据
uniqueVals=set(featValues)
for value in uniqueVals:
subLabels=labels[:]
#以当前最优特征划分出的各部分,继续向下递归:
myTree[bestFeatLabel][value]=createTree(splitDataSet
(dataSet,bestFeat,value),subLabels)
return myTree
myDat,labels=createDataSet()
createTree(myDat,labels)
#{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
2.4 绘图展示
#====================================================================绘图构造注解树
decisionNode=dict(boxstyle='sawtooth',fc='0.8')#决策节点的格式
leafNode=dict(boxstyle='round4',fc='0.8')#叶节点的格式
arrow_args=dict(arrowstyle='<-')#箭头的格式
def plotNode(nodeTxt,centerPt,parentPt,nodeType):
createPlot.ax1.annotate(nodeTxt,xy=parentPt,xycoords='axes fraction',
xytext=centerPt,textcoords='axes fraction',
va='center',ha='center',bbox=nodeType,
arrowprops=arrow_args)
def getNumLeafs(myTree):
numLeafs=0
firstStr=list(myTree)[0]
secondDict=myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
numLeafs+=getNumLeafs(secondDict[key])
else:
numLeafs+=1
return numLeafs
def getTreeDepth(myTree):
maxDepth=0
firstStr=list(myTree)[0]
secondDict=myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
thisDepth=1+getTreeDepth(secondDict[key])
else:
thisDepth=1
if thisDepth>maxDepth:
maxDepth=thisDepth
return maxDepth
#str(retrieveTree(1)).count('}')//2#这个数树深度的方式更取巧
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):
numLeafs = getNumLeafs(myTree)
depth = getTreeDepth(myTree)
firstStr = list(myTree)[0]
#下面这个计算cntrPt的方式书中没有解释,看上去让人很费解。
#其实这个cntrPt就是label的坐标,以一个起始叶子的坐标+移动的距离(就是那个1+numLeafs/2/totalW)
#为什么移动距离是这样计算的呢?
#那是一个叶子距离(1/totalW)加上由该label生长出的叶子们的中心距离((numLeafs-1)/totals/2)
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
#画节点和线的标签
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
plotTree(secondDict[key],cntrPt,str(key)) #recursion
else:
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD#递归返回上级时,恢复yOff的坐标,以便继续绘图
def createPlot(inTree):
fig = plt.figure(1, facecolor='white',figsize=(7,5))
fig.clf()
axprops = dict(xticks=[], yticks=[])#指定刻度的可选参数
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #no ticks
#createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5/plotTree.totalW#起始位置是按照将1均分成(总宽度)份,然后左右就各自多出一份的一半
plotTree.yOff = 1.0;
plotTree(inTree, (0.5,1.0), '')
plt.show()
用决策树字典{'no surfacing':{0:'no',1:{'flippers':{0:'no',1:'yes'}}}}测试该绘图函数,结果如下:
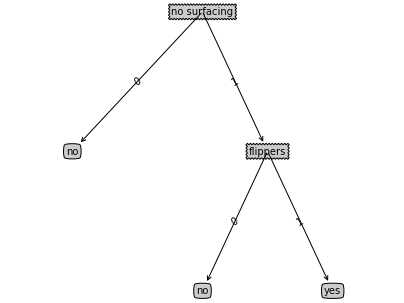
图挂了这个故事告诉我们减少对第三方免费服务的依赖,文件能自己存就自己存,功能能代码实现就用代码实现。
2.5 预测新样本类别
#===================================================利用训练好的决策树进行新样本的分类
def classify(inputTree,featLabels,testVec):#后两个参数的属性顺序要一一对应
firstStr=list(inputTree)[0]
secondDict=inputTree[firstStr]
featIndex=featLabels.index(firstStr)
for k in secondDict.keys():
if testVec[featIndex]==k:
if type(secondDict[k]).__name__=='dict':
classLabel=classify(secondDict[k],featLabels,testVec)
else:
classLabel=secondDict[k]
return classLabel
Ps.可使用pickle模块存储决策树,以便训练完以后再次使用。
#==========================================================使用pickle模块存储决策树
def storeTree(inputTree,filename):
import pickle
with open(filename,'w') as fw:
pickle.dump(inputTree,fw)
def grabTree(filename):
import pickle
with open(filename) as fr:
return pickle.load(fr)
3 示例
以书中第3章给出的隐形眼镜数据集来展示算法的效果:
#=======================================================示例:使用ID3预测隐形眼镜类型
with open('/Users/fuyangzhen/Documents/machinelearninginaction/Ch03/lenses.txt') as fr:
lenses=[inst.strip().split('\t') for inst in fr.readlines()]
lensesLabels=['age','prescript','astigmatic','tearRate']
lensesTree=createTree(lenses,lensesLabels)
createPlot(lensesTree)
得出的决策树的字典如下:
{'tearRate': {'normal': {'astigmatic': {'no': {'age': {'pre': 'soft',
'presbyopic': {'prescript': {'hyper': 'soft', 'myope': 'no lenses'}},
'young': 'soft'}},
'yes': {'prescript': {'hyper': {'age': {'pre': 'no lenses',
'presbyopic': 'no lenses',
'young': 'hard'}},
'myope': 'hard'}}}},
'reduced': 'no lenses'}}
得出的决策树的注解树如下:
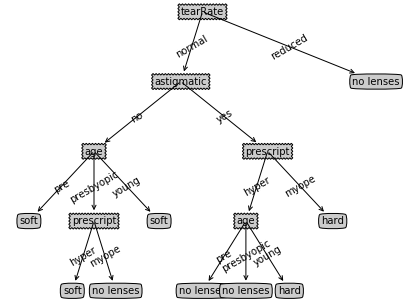
4 小结
决策树能非常好地匹配标称型实验数据,但可能存在匹配选项过多地现象,即过度匹配(overfitting)。为了减少过度匹配问题,可以裁剪决策树,去掉一些不必要的叶节点:若叶节点智能增加少许信息,则可以删除该节点,将它并入导其他叶节点中。
决策树分类器就像带有终止块的流程图,终止块表示分类结果。开始处理数据集时,我们先需要测量集合中数据整体的不一致性(熵),然后寻找最优特征来划分数据集,直到数据集中所有数据属于同一分类。